Notable Features
Combining expressivity and simplicity
Athena is based on multi-sorted first-order logic augmented with Hindley-Milner-style polymorphism. This is a very expressive and versatile logic that remains conceptually simple and computationally tractable.
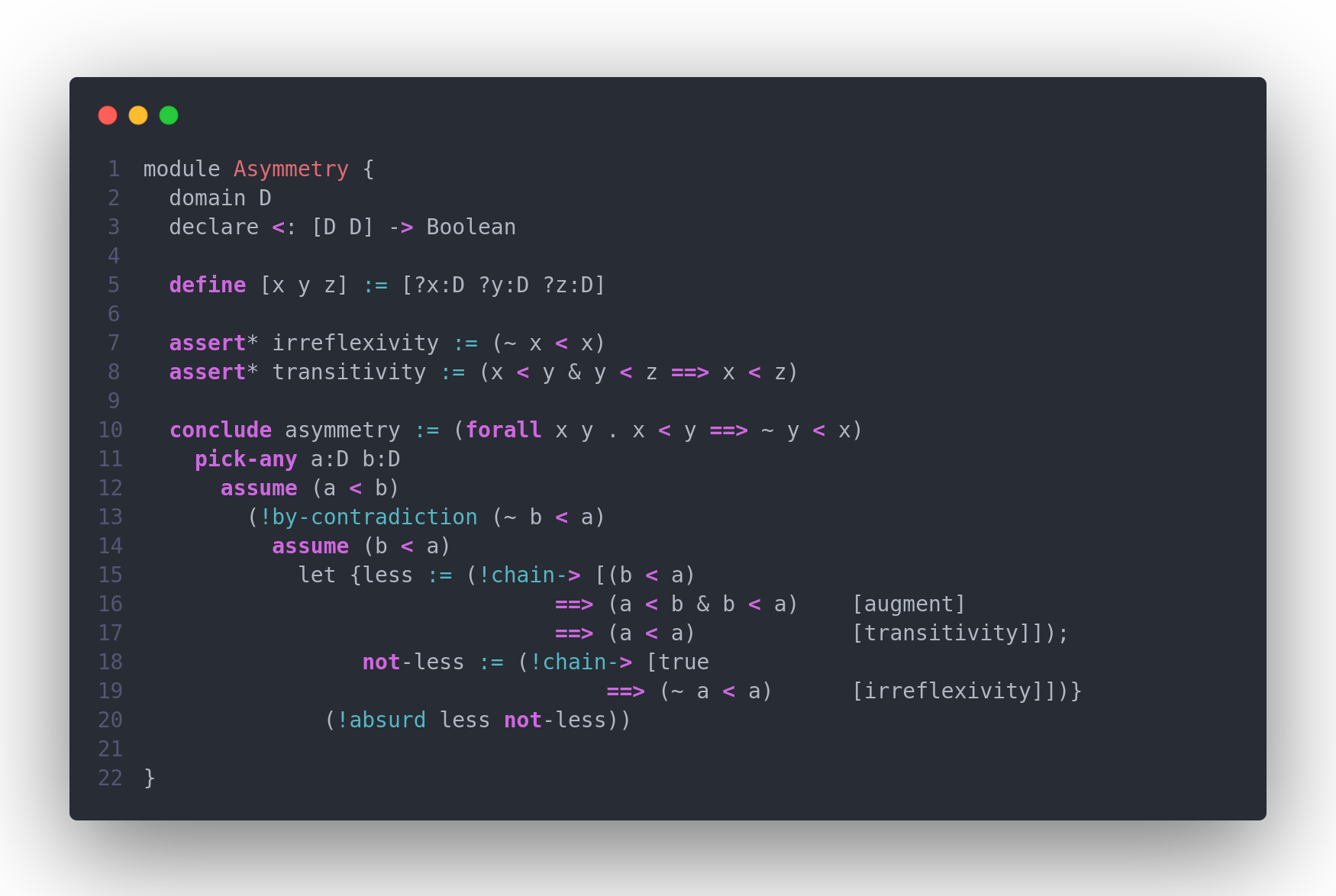
True natural-deduction style
Proofs are written in a natural-deduction notation that resembles the style of the informal proofs that scientists and engineers write in practice. Assumption scope is modeled by built-in syntax forms with custom semantics, based on the notion of assumption bases.
Conditional and Equational Rewriting
Athena's conditional-rewriting subset enables users to write executable formal specifications of systems and to search for counterexamples automatically.
Built-in Proof Automation
Athena ships fully integrated with industrial-strength reasoning systems: SAT solvers (such as CaDiCaL and MiniSat), SMT solvers (such as CVC4, Z3, and Yices), automated theorem provers (ATPs) such as SPASS and Vampire, Prolog engines, and more.
Proof Reuse and Custom Tactics
Unlike many proof assistants, Athena does not require that custom proof tactics be developed in a second language. Deductions are first class citizens in Athena, making proof reuse and abstraction far more ergonomic.
Flexible Module System
Athena's module system makes it easy to organize large-scale proofs.
Extensible notation
Athena offers the usual mechanisms for customizing syntax, such as operator overloading, custom precedence and associativity levels, and so on. But it goes beyond these with powerful new features, such as input expansions and output transformations, that can radically simplify notation.
Abstract-level proofs and structured theories
Abstract proofs are akin to generic algorithms. Athena has a built-in implementation of abstract structures as collections of polymorphic operators and theories, as well as theory refinement and evolution. Abstract structures can be specialized to many different concrete structures through adaptation with operator mappings.